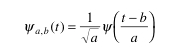
本研究では、空間分解能を確保しつつ画像処理を行うためにウェーブレット変換
を用い、ダウンサンプリング後の失われた情報の捕間を行う手法を提案する。
先頭に戻る
STFTをするために、ある特定の区間で非0となるステップ関数を用いる。 この用な関数を窓関数と呼び、ある区間に窓をかぶせてその部分だけの内積を求め、 窓をかぶせた部分以外ははこの場合無視される。これで特定の区間の周波数分布を分析する事が出来る。
しかし、難点もある。一般的に信号は、様々な周波数が含まれ、 高い周波数の場合は、十分な周波数分解能を得るために必要な窓の長さは短く、低い周波数の場合は、十分な周波数分解能を得るためには、より長い窓が必要になる。窓を長く取ると、時間分解能が下がるため周波数分解能と時間分解能は同時には向上させることは出来ないというトレードオフが発生する。
この不確定性においてウェーブレット変換を使う利点は、「時間周波数の 窓の面積は変えられなくても、運動に応じて時間周波数の窓の形を変える必要 がある」という点である。 時間周波数の窓の形は、窓関数だけから決まってしまい、形を変えるには 窓関数を替えなければならない。どのように取り替えたらよいのだろうか。 そのひとつの答えがここで述べる連続ウェーブレット変換である。
ウェーブレットは波の基本単位として用いられ、Ψ(t)で 表現する。 ウェーブレット関数は2つの実数パラメータa,bを使って
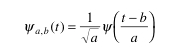
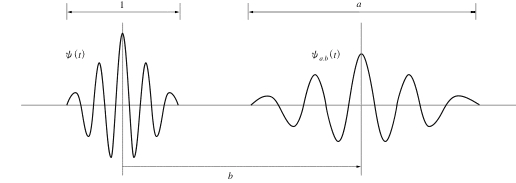
大きさは1/√a倍されるが、エネルギー的に一定を保つために必要。 aはスケール(scale)と呼ばれ、ウェーブレットの時間幅を表している ので1/aは周波数に相当する。ここで、横軸関数をxとし、任意の信号f(x) とウェーブレット関数Ψ_a_b(x)との内積
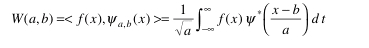
特に、画像データの各バンド内の個々のピクセル値(放射量)を使って画像を判読し易くすることを「画像強調」と呼ぶ。Histogram Equalizationは非線形な画像強調の一つで、範囲(レンジ)内の各値を持ったピクセルの数がほぼ一定になるように、ピクセルの値を再配分する。
その結果、ヒストグラムの形は平坦に近くなり、「ピーク」付近のコントラストの 増加、「末端」のコントラストは低下する。そうした出力画像は、全体的に コントラストがはっきりした見易い画像となる。
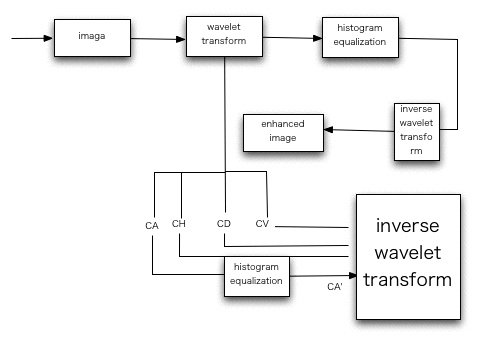
この研究は、時間分解能と周波数分解能のトレードオフの中で、最適な手法を探し画像強調を最適化する。
[1]「ウェーブレット解析の基礎理論」新井康平著
先頭に戻る